This is part two of a developer diary series on building a data splitter for Abzu’s python library Feyn® and the QLattice®. You can read part one here if you haven’t already. Building on top of the decisions in the previous post, I’ll share some of the design choices in getting multiple stratification right.
Getting stratification right.
For stratification, we have a few requirements we want to meet:
- We can fairly stratify among multiple columns
- We treat missing (NaN) values as a distinct value and distribute them proportionally as well
- We maintain the resulting sizes of the splits after stratifying on as many columns as possible.
- We give actionable errors to the user when a split is not possible due to a stratification choice.
This includes telling which column or combination is not prevalent enough to split into the provided splits (or ratios).
Multiple columns.
We want to support multiple stratification, so we start with grouping the data frame by each of the columns.
As an example for a binary column, this would create a dataframe with two groupings:
- The samples where the value is 1 (or True)
- The samples where the value is 0 (or False)
The primary consideration is ensuring that the samples are distributed fairly among the desired bucket sizes. The most common solution is to shuffle the samples to avoid accidental homogeneity in your subsets due to ordering.
It’s worth mentioning that other tools often make shuffling the data optional.
We make the conscious choice to always shuffle, since forgetting to shuffle the data is a common mistake that can result in a worse model and a poor view of its performance.
Always shuffling helps mitigate the sensitivity of the initial ordering of the data set.
This expands combinatorially for each column you add, which limits how many columns you can stratify for, depending on the distribution of the values and how many samples you have.
As an example, we can add a categorical column to the previous grouping. This column contains three distinct values, **’Apple’**, **’Banana’** and **’Orange’**. That means we would have to proportionally ensure that all combinations are present for each subset, like this
- (1, Apple)
- (0, Apple)
- (1, Banana)
- (0, Banana)
- (1, Orange)
- (0, Orange)
We call these groupings `strata`, and each of them is a `stratum`.
The splitting algorithm.
Let’s take a second to recall the simplified algorithm from part 1:
` ` `
For each ratio in the list:
- Compute the number of samples the set should contain for the ratio, rounded up to the nearest integer.
- Choose a random subset and subtract the difference due to rounding, if any
- Finally split the dataset using the computed sizes
` ` `
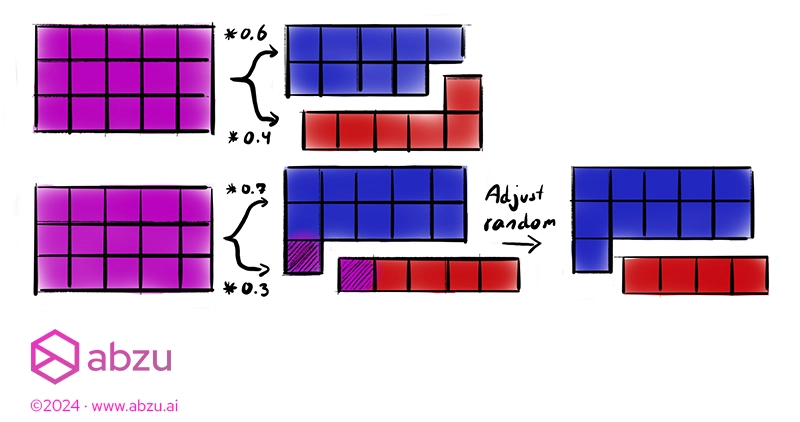
The picture above shows the process for even and uneven splits.
Satisfying the ratio evenly.
With the groupings, we apply the same algorithm as above for each stratum and finally merge the results into the subsets.
There’s a few reasons why we take this approach:
- We guarantee each stratum has samples represented in each subset.
- The behaviour is consistent whether you stratify or not.
- We get to use the same logic for all cases, which is simpler to maintain and test
- We can produce a meaningful error if a combination does not contain enough samples to give at least one for each subset.
The downside is that in rare cases, one subset might get all the random adjustments. This is mostly an issue for small datasets, and we make sure to give a warning if the ratios get skewed.
` ` `
For each stratum:
- Split the index locations for each stratum into stratum-subsets like in the simple algorithm above.
- Adjust a random stratum-subset due to rounding as necessary
- Merge each of the strata-subsets for each subset
- Finally split the dataset by the indices for each subset
` ` `
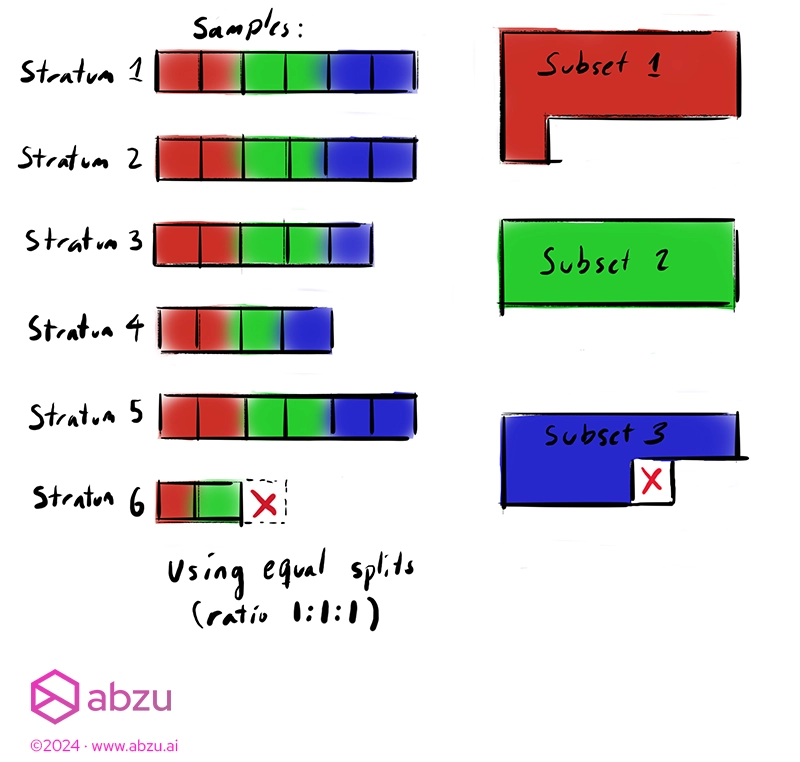
A note on small datasets with many subset splits
When choosing to perform many splits of very different ratios for small datasets, not every subset may contain enough samples for the adjustment required after rounding.
This is not likely to happen with regular splitting, but it does become important when we go into stratification where the individual stratum can be small.
To solve this, we distribute the differences among multiple sets with an adjusted algorithm:
` ` `
Keep a list of candidates.
While the list of candidates is empty:
- For each subset:
- If the length is large enough to be adjusted, add it as a candidate
- If no candidates are found, halve the adjustment and try again
- If the adjustment can’t be lowered further, return an error; the dataset does not support the amount of splits specified by the user.
When there are candidates:
- Pick a random subset only among the candidates and subtract the difference due to rounding
Finally split the dataset using the computed sizes
` ` `
This could be improved where no split gets the majority of the difference but since this is an edge case, we favor the simple approach.
Instead, we produce a warning if the adjustment ends up skewing the ratios, and we notify the user if the split is not possible to perform.
Wrapping up!
That’s it for the journey of creating a data splitter with stratification for `Feyn`.
Software is never really done and requirements can change in the future, but until then I hope this little walkthrough of the design process was helpful or at least entertaining to read.
Kevin Broløs.
Kevin is Abzu’s Mad Scientist and expert on the QLattice®. With a solid foundation in high-performance computing, his work ensures our tools are at the cutting edge of AI and data science.
More by Kevin:
